Geometry.ru

Как? и Зачем?

И. Ф. Шарыгин. Нужна ли в школе 21-го века Геометрия? (pdf)
Матем. просв., сер. 3, 8, 2004 г.

А. Д. Блинков. Почему я не вызываю учеников к доске?(doc)
Статья написана в 2004 году к Международному конгрессу по образованию.

И. А. Кушнир. Эмоциональная геометрия (pdf)
Эмоциональная геометрия основана на коротких посильных и красивых задачах повышенной сложности. О таких задачах (в том числе, авторских) и пойдет речь.

И. Ф. Шарыгин. Избранные статьи djvu.

Статьи Игоря Фёдоровича в "Кванте" .

В. Протасов, В. Тихомиров. Геометрические шедевры Шарыгина (pdf) "Квант", №1, 2006 г.

Cредняя линия. Параллелограмм

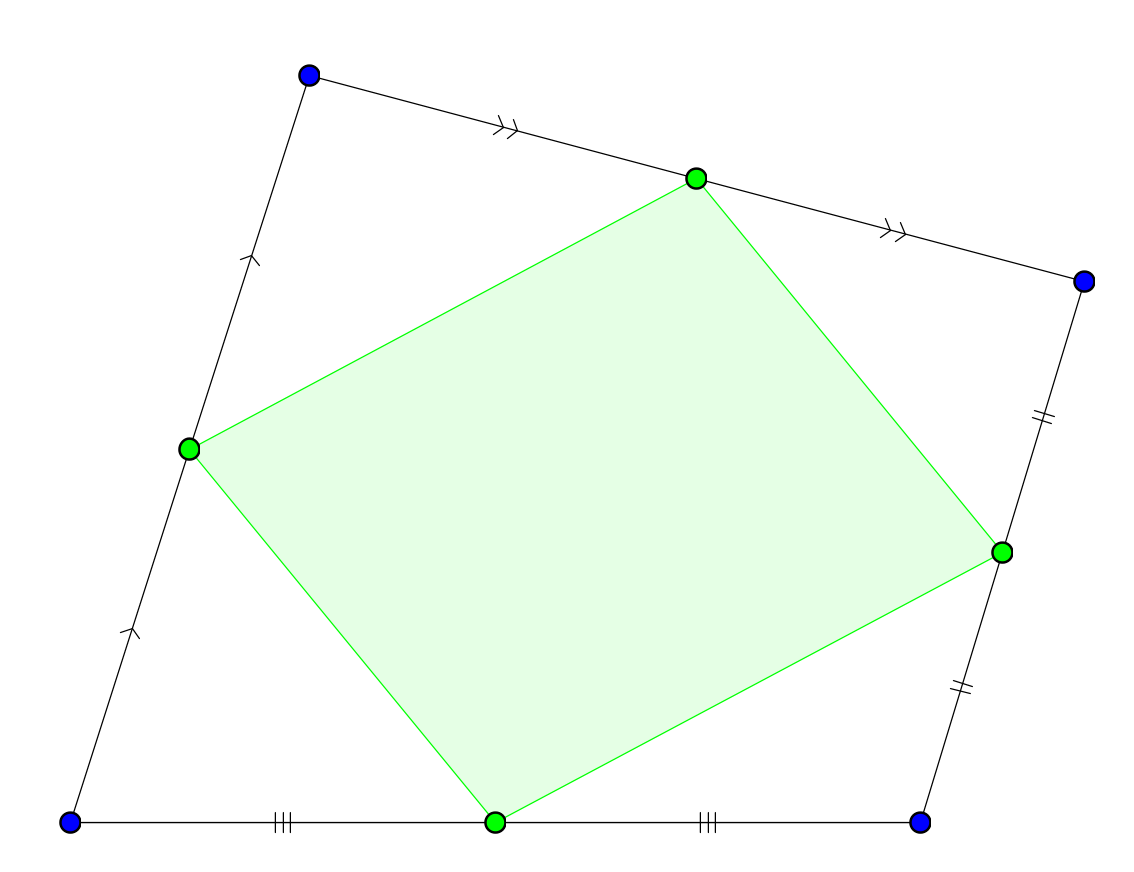
Г. Б. Филипповский. Параллелограмм Вариньона решает задачи

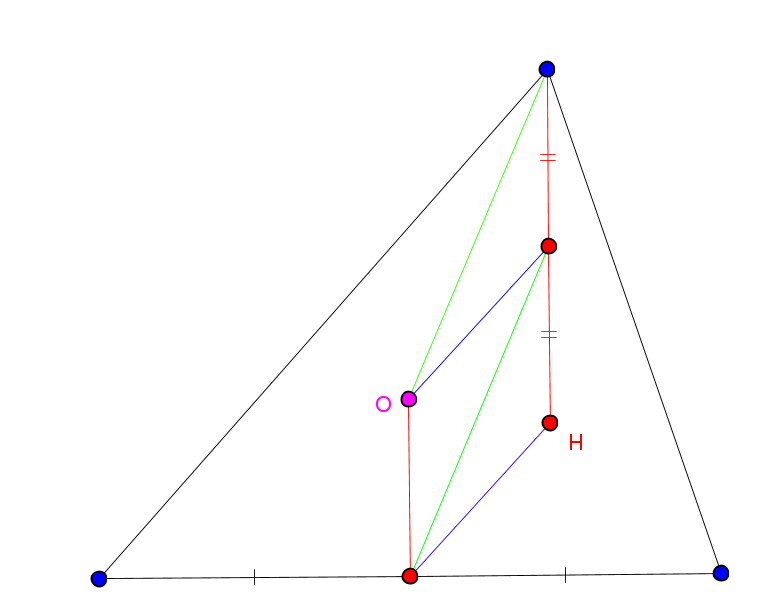
Г. Б. Филипповский. О двух параллелограммах в треугольнике. (pdf) "Квант", №4, 2008 г.

Квадраты

Е. Бакаев. Комбинации квадратов (pdf). "Квант", №7, 2018г.

А. Д. Блинков, Ю. А. Блинков. Угол в квадрате (pdf). "Квант", №4, 2015 г.

Е. Бакаев, А. Д. Блинков. Вспомогательные квадраты (pdf). "Квант", №4, 2016 г.

Вокруг биссектрисы

И. Ф. Шарыгин. Вокруг биссектрисы "Квант", №8, 1983 г.
"В этой статье собраны некоторые геометрические факты, прямо или косвенно связанные с биссектрисой треугольника."

Г. Б. Филипповский. К вопросу о событиях на одной прямой l

Г. Б. Филипповский. Точка Q – основание внешней биссектрисы

Теорема Штейнера-Лемуса

А. Коробов. Семь решений задачи Штейнера. "Квант", №4, 1996 г.

Л. Штейнграц. Новый взгляд на теорему Штейнера-Лемуса. (pdf) "Квант", №1, 2013 г.

Вписанная и вневписанные окружности

А.Д. Блинков, Ю.А. Блинков. Вневписанная окружность. (pdf) "Квант", №2, 2009 г.
В статье излагаются классические факты о вневписанной окружности, обсуждаются задачи, в которых вневписанная окружность возникает самым неожиданным образом.

Г. Б. Филипповский. Замечательная прямая треугольника. (pdf) "Квант", №4, 2007 г.
К статье рекомендуем подборку задач о вписанной окружности.

Ю. Билецкий, Г. Филипповский. О пользе вневписанных окружностей. (pdf)

"Квант", №2, 2001 г.

А. Д. Блинков, Ю. А. Блинков. Две окружности в треугольнике, три окружности в треугольнике... (pdf) "Квант", №2, 2012 г.

А.А. Заславский, М. Панов О вписанной окружности прямоугольного треугольника (pdf) "Квант", №4, 2017 г.

П. А. Кожевников. Вневписанные окружности и дюжины точек.
21-я летняя конференция международного математического Турнира городов.

Фольклор Задача Ф. Ивлева. (pdf)
В заметке решение трудной и красивой задачи разбито на несколько подзадач, что позволяет использовать материал на кружке. Решения многих задач и различные обобщения можно найти в статье.

Huseyin Demir and Cem Tezer More on Incircles (pdf) Mathematics Magazine, Vol. 62, No. 2 (Apr., 1989), pp. 107-114

Площадь

Е. Бакаев. Площадь Треугольника (pdf)

"Квантик №2", 2012 год

А. Щетников. Параллелограмм и равенство площадей (pdf)

"Квантик №2", 2012 год

Прямая Эйлера и окружность девяти точек

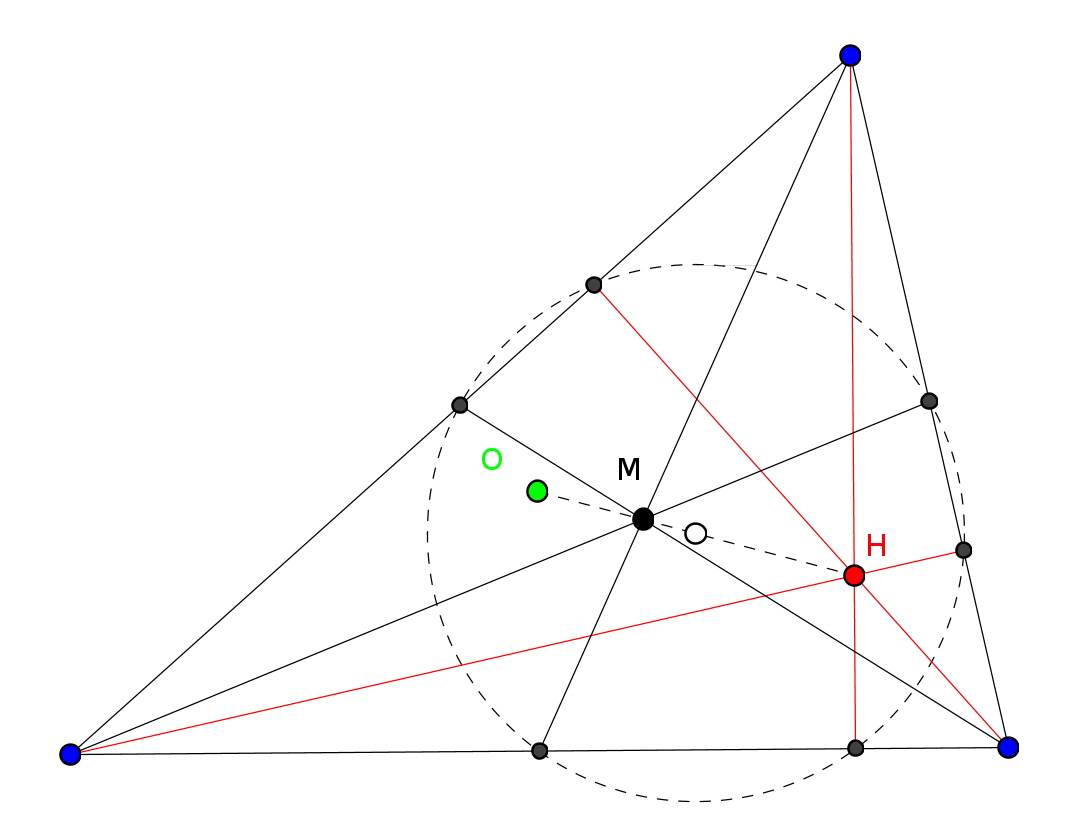
И. Ф. Шарыгин, А. Ягубьянц. Окружность девяти точек и прямая Эйлера "Квант" №8, 1981 г.
К этой статье рекомендуем такую серию задач.

И. А. Кушнир. Золотой ключ Леонарда Эйлера (pdf) "Математика в школах Украины", №13-15, 2012 г.
Рассказывается о приложениях окружности девяти точек для доказательства классических задач.

Д. В. Швецов. Важная лемма (pdf) "Квант" №5-6, 2012 г.

Л. А. Емельянов. Точка Шиффлера (pdf) "Математика в школе" №6, 2006 г.
Пусть $I$ – центр вписанной окружности треугольника $ABC$. Тогда прямые Эйлера треугольников $AIC$, $AIB$, $BIC$, $ABC$ пересекаются в одной точке!

Nguyen Minh Ha. A proof of Vittas’ Theorem and its converse (pdf)
Во вписанном четырёхугольнике $ABCD$ диагонали пересекаются в точке $P$. Тогда прямые Эйлера треугольника $APB$, $BPC$, $CPD$, $DPA$ пересекаются в одной точке.

Debdyuti Banerjee and Sayan Mukherjee. Neuberg Locus And Its Properties (pdf) Journal of Classical Geometry, Volume 2, 2013
Отметим все такие точки $P$, что прямые Эйлера треугольников $APB$, $BPC$, $CPA$ пересекаются в одной точке. Оказывается, что это ГМТ обладает многими интересными своствами.

Точка Микеля, прямая Симсона, прямая Штейнера, теорема Дроз-Фарни

Ю. А. Блинков. Точка Микеля(pdf)
Базовые факты о точке Микеля.

Michal Rol ́ınek and Le Anh Dung The Miquel Points, Pseudocircumcenter, and Euler-Poncelet Point of a Complete Quadrilateral (pdf), Forum Geometricorum Volume 14 (2014) 145–153.

Г. Б. Филипповский. Ґрунтовна розмова про пряму Симсона-Уоллеса
Увлекательный рассказ о всех основных свойствах прямой Симсона, разбирается большое количество примеров!

Д. В. Швецов. От прямой Симсона к теореме Дроз-Фарни (pdf)
Журнал "Квант", №6, 2010 г.

Е. Д. Куланин. О прямых Симсона, кривой Штейнера и кубике Мак-Кэя (pdf)
Ежегодник «Математическое просвещение», №10, М., 2006
Обстоятельная статья, в которой, например, изучается вопрос касания прямых Симсона окружности Эйлера.

Cosmin Pohoata and Son Hong Ta. A Short Proof of Lamoen’s Generalization of the Droz-Farny Line Theorem (pdf)
Теорему Дроз-Фарни можно обобщать в разных направлениях. Об одном таком и идёт речь в статье.

Titu Andreescu and Cosmin Pohoata Droz-Farny Demystified (pdf)
В статье приводится очень короткое доказательство красивого обобщения теоремы Дроз-Фарни.

Теорема Фейербаха и точка Фейербаха

В. Ю. Протасов. Касающиеся окружноти: от Тебо до Фейербаха. (pdf) "Квант", №4, 2008 г.
В статье обсуждаются сразу две жемчужины: теорема Тебо и теорема Фейербаха. Оказывается, что одна из теорем является следствием другой!

П.А. Кожевников. Ещё раз о точке Фейербаха. (pdf) Математическое просвещение, Выпуск 15, 2012 г.
"В этой заметке предлагается геометрическое доказательство теоремы Фейербаха, которое дает возможность описать точку Фейербаха и, в частности, получить отличное от авторского геометрическое решение задачи 8 из задачного раздела «Математического просвещения», вып. 14, 2010 г."

J.L. Ayme. Красивое доказательство теоремы Фейербаха. (pdf)
Очень красивое доказательство теоремы Фейербаха. Оригинал статьи можно посмотреть на странице автора.

Фольклор. Доказательство теоремы Фейербаха по И. Ф. Шарыгину. (pdf)

Nguyen Minh Ha and Nguyen Pham Dat. Synthetic Proofs of Two Theorems Related to the Feuerbach Point.(pdf) Forum Geometricorum Volume 12 (2012) 39–46.
В статье излагаются геометрические доказательства двух замечательных теорем, связанных с точкой Фейербаха. Кроме цитированной статьи J. Vonk, рекомендуем заглянуть в статью Куланина Е. Д., в которой теорема Емельянова доказывается с помощью коник.

Jan Vonk. The Feuerbach point and reflections of the Euler line. (pdf) Forum Geometricorum, 9 (2009) 47--55.
Рассматриваются интересные свойства точки Фейербаха.

Куланин Е.Д., Шихова Н.А. Прямые Эйлера и точки Фейербаха.(pdf)
Математическое образование, №2, 2012.

Кожевников П. А.(по статье Д. Гринберга) Обобщение теоремы Фейербаха. (pdf)

Куланин Е. Д. Об описанных окружностях чевианных и педальных треугольников и некоторых кривых, связанных с треугольником. (pdf)
Ежегодник «Математическое просвещение», №9, М., 2005.
Доказательство теоремы Фейербаха через коники! В статье указывается целое семейство окружностей, проходящих через точку Фейербаха(например, окружность, проходящая через основания биссектрис, проходит через точку Фейербаха). Для понимания статьи необходим некоторый опыт работы с кониками, который можно получить, почитав замечательную книгу А. Акопяна, А. Заславского (pdf).

Симедиана

А. Карлюченко, Г. Филипповский. О касательных, проведённых в двух вершинах треугольника , (pdf)

Ю. Блинков. Симедиана (pdf), "Квант", №4, 2015 г.

Tran Quang Hung . A Simple Synthetic Proof of Lemoine’s Theorem (pdf)

Конструкции

В.Ю. Протасов. О двух велосипедистах и вишнёвой косточке (pdf) "Квант", №3, 2008 г. "Попробуем подвести некоторые итоги. Две задачи международных олимпиад, задача о бабочке, два десятка геометрических задач, которые мы сформулировали в виде упражнений (некоторые из них появлялись на математических олимпиадах, в Задачнике <Кванта>, и в различных сборниках задач). Список далеко не полный. И все это выросло из задачи 1, совсем простенькой и неинтересной, которую мы вначале и решать-то не хотели."

Г. Б. Филипповский. О точке на стороне и двух параллельных (pdf) "Математика в школах Украины", №4, 2011 г.

А. Полянский. Воробьями по пушкам (pdf) "Квант", №2, 2012 г. Решения упражнений
"В этой статье мы пользуясь двумя простыми и элегантными фактами, решим две достаточно сложные задачи."

Ю. А. Блинков Ортоцентр, середина стороны, точка пересечения касательных и ещё одна точка ! (pdf) "Квант", №2, 2014 г.

А. Карлюченко, Г. Филипповский. Задачи с тремя равными окружностями (pdf) "Математика в школах Украины", № 22-23, август 2014 г.

Г. Б. Филипповский. "Угловые" приключения барона Мюнхгаузена (pdf)

А. Карлюченко, Г.Б. Филипповский. Про вiдстанi вiд вершини трикутника до його чудових точок (pdf). "У світі математики", том 22, випуск 4, 2016 г.

Ф. Нилов. New Examples of Hexagonal Webs of Circles (pdf)

Задача о бабочке

А. В. Спивак. Десять бабочек (pdf)

Е. С. Горская. Шесть доказательств теоремы о бабочке (pdf) Сборник "Учим математике-2". МЦНМО, 2009 г.

Построения

Г. Б. Филипповский, А. Карлюченко На трёх параллельных прямых pdf

А. Д. Блинков Геометрические построения с помощью треугольника-шаблона (pdf) "Квантик", №3-4, 2012 г.

Е. Д. Куланин Еще раз о трисекции угла (pdf) "Математика в школах Украины", №4, 2012 г.

Гомотетия

Б. Гейдман. Гомотетия и замечательные точки в треугольнике "Квант", №10, 1977 г.

А. Спиров. Неожиданная поворотная гомотетия (pdf) "Квант", №5, 1998 г.

П. А. Кожевников. Задача M2100 (pdf)

Рекомендуем такие интересные серии задач на гомотетию:

Ортоцентр, середина стороны, точка пересечения касательных и … еще одна точка! (pdf)

Прямая Нагеля (pdf)

Лемма о вписанной окружности

Поворотная гомотетия

Полувписанная окружность, окружности Тебо

А. Гирич. Несколько задач о треугольниках и окружностях "Квант", №11, 1990 г.

В. Ю. Протасов. Касающиеся окружноти: от Тебо до Фейербаха. (pdf) "Квант", №4, 2008 г.

Рекомендуем серию задач про полувписанную окружность:
полувписанная окружность

А. Львов. О центрах гомотетий вписанных окружностей и окружностей Тебо pdf

Wilfred Reyes. An Application of Thebault’s Theorem (pdf) Forum Geometricorum Volume 2 (2002) 183–185.

Dmitry S. Babichev. Circles touching sides and the circumcircle for inscribed quadrilaterals (pdf) Journal of Classical Geometry, Volume 1, 2012

Замечательные окружности

Г. Б. Филипповский. "Досье" на окружность Аполлония

Очень советуем порешать замечательную подборку задач Д. В. Прокопенко.

А. Г. Мякишев. Прогулки по окружностям: от Эйлера до Тейлора(pdf)

Jan Vonk and J. Chris Fisher. On a new circle associated with a triangle (pdf) Forum Geometricorum Volume 11 (2011) 13–26.
В статье, посвящённой окружности Фурмана, очень много красивых геометрических доказательств.

Трисекция. Теорема Морлея

Л. Штейнгарц Снова о теореме Морлея "Квант" №5, 2009 год.

Л. Емельянов, Т. Емельянова Теорема Морлея. Сто лет спустя "Математика в школе", 2004 год.

Г. Б. Филипповский Трисекция угла в задачах школьной геометрии

Тоноян Г., Яглом И. Теорема Морлея "Квант" №8, 1978 год.

Е. Д. Куланин Еще раз о трисекции угла (pdf) "Математика в школах Украины", №4, 2012 г.

Изогональное сопряжение

Для первого знакомства с темой рекомендуем книжку В. В. Прасолова и статью Д. Гринберга(ниже).

Д. Гринберг. Isogonal conjugation with respect to a triangle (zip)

А. В. Акопян, А. А. Заславский. Разные взгляды на изогональное сопряжение (pdf) Математическое просвещение, сер. 3, вып. 11, 2007.

Д. В. Прокопенко Изогональное сопряжение и педальные треугольники pdf "Квант" №9, 2017 год.

А. Куликова, Д.В. Прокопенко Теорема об изогоналях pdf , "Квант", №4-5, 2018 год
" В статье приведено доказательство теоремы и продемонстрирована эффективность применения этой теоремы в олимпиадных задачах высокого уровня"

А. Уткин Изогональное сопряжение в четырехугольнике pdf, "Квант", №2, 2019 "В этой статье мы расскажем об изогональном сопряжении в четырехугольнике и покажем, что оно может оказаться полезным при решении задач"

Dimitar Belev. Some Properties of the Brocard Points of a Cyclic Quadrilateral (pdf), Journal of Classical Geometry, volume 2, 2013

A. В. Акопян. Conjugation of lines with respect to a triangle (pdf), Journal of Classical Geometry, volume 1, 2012
В статье речь идёт об обобщениях изогонального и изотомического сопряжениях. Для понимания статьи нужны знани проективных преобразований и коник. Всё необходимое можно найти в книжке про коники.

Теорема Кэзи

Luis Gonzlez. Casey’s Theorem and its Applications (pdf)

Shay Gueron. Two Applications of the Generalized Ptolemy Theorem (pdf)

Shailesh Shirali. On the Generalized Ptolemy Theorem (pdf)

Л. Емельянов. Замечательная окружность (pdf)

Комбинаторная геометрия

В. Ю. Протасов Теорема Хелли и вокруг неё (pdf) "Квант", №3, 2009 г.

Н. Б. Васильев Формула Пика "Квант", №12, 1974 г. Для дальнейшего знакомства с этим сюжетом рекомендуем книжку Вавилова и Устинова "Многоугольники на решетках"(pdf).

А. Полянский Одной рукой узелок не развяжешь ! (pdf) "Квант" №3, 2013 год.

Н. Б. Васильев Сложение фигур "Квант", №4, 1976 г.

А. Спивак, М. Смуров Покрытие полосками (часть-1) и (часть-2) "Квант", №4-5, 1998 г.

М. Петкова Салфетки "Кванта" и теорема Пифагора (pdf) "Квант" №3, 2012 год.

С. Табачников, В. Тиморин Прямая Сильвестра(pdf) "Квант", №5, 2009 г.

Геометрические неравенства

В. Протасов, В. Тихомиров Пространство Lp и замечательные точки треугольника (pdf) "Квант", №2, 2012 г.

Claudi Alsina, Roger B. Nelsen. Геометрическое доказательство неравенства Эрдеша-Морделла.(pdf)
Forum Geometricorum, 7 (2007) 99-102. В статье излагается одно из самых красивых доказательств известного неравенства.

Замечательные кривые

Акопян А. В. Кардиоида. "Квант" №3, 2012 год.

Акопян А. В. Лемниската Бернулли "Квант" №3, 2009 год.

Теорема Понселе

Протасов В. Ю. Два века теоремы Понселе (pdf), Журнал "Квант" №5-6, 2014 г.

Протасов В. Ю. Обобщенные теоремы о замыкании (pdf) / Generalized closing theorems (pdf)

Е.Диомидов, А.Заславский, В.Калашников, Г.Челноков. Вокруг теоремы Понселе. Материалы ЛКТГ, 2014 г.

Белухов Н. И. The Mixed Poncelet-Steiner Closure Theorem. (pdf)

Алгебра и геометрия

Г. Б. Филипповский. Рене Декарт (1596–1650). Декартова система координат (pdf) "Математика в школах Украины", №35-36, 2011 г.

А.И. Сгибнев. «Геометрия помогает алгебре» (ps, 2M), (ps-zip, 400K), (pdf, 190K)

Стереометрия

В.Ю. Протасов. Выход в пространство-2 pdf "Квант" №1-2, 2018 г.

С. Кузнецов. Расстояния на сфере pdf "Квант" №4, 2017 г.

В. Дубровский, В. Матизен. Из геометрии тетраэдра "Квант" №9, 1988 год.

А. Заславский. Описанная и вписанные сферы тетраэдра "Квант" №1, 2004 год.

А. Заславский, Д. Косов. Изогонально сопряжение в тетраэдре и его гранях "Квант" №3, 2004 год.

Нам пишут

В этом подразделе представлены тексты, присланные в редакцию сайта.

Е. И. Галахова. Девочка на шаре. pdf

"Пусть на описанной окружности треугольника ABC взята точка X. Окружность ω, проходящая через точки B и X пересекает стороны BC и AB (или их продолжения) в точках D и E соответственно. Тогда, в зависимости от условий, накладываемых на точку X или окружность ω, можно определить конструкции, значительно упрощающие поиск решения соответствующих задач."

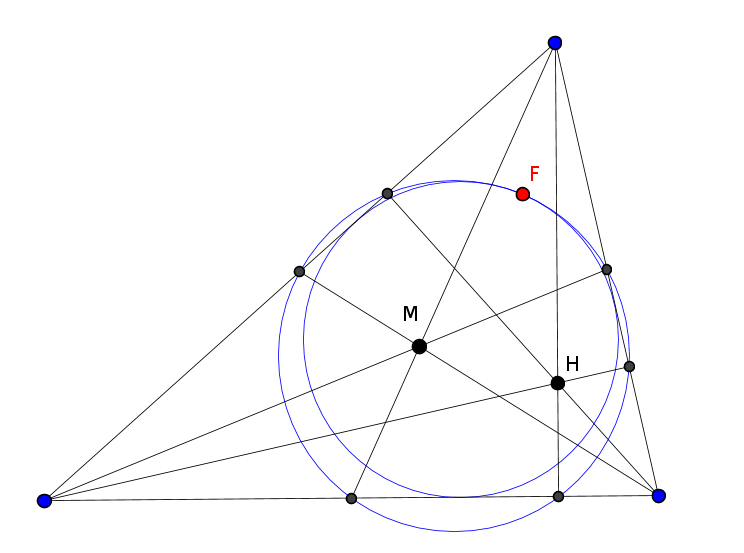
К. Бельский. Обобщение леммы Веррьера pdf

"Дан треугольник △ABC с центром вписанной окружности I. Окружность wa касается сторон AB,AC и окружности (ABC) в точках F,E,T соответственно. Ma середина дуги BAC окружности (ABC). Тогда I середина отрезка EF и точки T, I, Ma лежат на одной прямой."

К. Бельский. Теорема Дезарга об инволюции для вписанных и вневписанных окружностей треугольника. pdf

В статье обсуждаются некоторые приложения теоремы Дезарга об инволюции. Предполагается знакомство с основами проективной геометрии.

К. Бельский. Изогональное сопряжение и частный случай точек Микеля. pdf

"В треугольнике △ABC (P,Q) - пара изогонального сопряжения. Пусть X точка на прямой PQ. Точка X′ - изогонально сопряжена точке X в треугольнике △ABC. Пусть E, F пересечение окружностей (ABC) и (X′P Q). (из утверждений ниже будет следовать, что эти окружности всегда пересекаются, что само по себе интересно)В этой статье будут показаны свойств точек E,F для любой точки X, также будут рассмотрены частные случай точки X и пар точек (P, Q)."

С.С. Комаров. Две равные вписанные окружности в прямоугольном треугольнике pdf

"Точка D выбрана на гипотенузе AB прямоугольного треугольника ABC так, что окружности, вписанные в треугольники ACD и BCD, имеют равные радиусы. Назовём центры этих окружностей P и Q соответственно, а середину AB обозначим через M. Определим точки K и L как пересечения прямой, проходящей через M параллельно CD, с прямыми PC и QC соответственно. Обозначим точку пересечения, отличную от C, описанных окружностей треугольников ABC и PCQ через U. Тогда описанные окружности треугольников AKP и BQL касаются в точке U."

К. Бельский. Треугольники с общим ортоцентром и общей вписанной коникой pdf

"Дана коника $\Omega$ и точка $O$ вне её. Прямая $l$ --- касательная к конике $\Omega$, не проходящая через $O$. Прямые $l_1,l_2$ --- касательные из точки $O$ к конике $\Omega$. Точка $H$ --- ортоцентр треугольника, который образован прямыми $l,l_1,l_2$. Найти геометрическое место точек $H$ при изменении прямой $l$."