Все треугольники равносторонние. Докажем, например, что в произвольном треугольнике любые две стороны равны. Разгадку этого парадокса и другие геометрические софизмы Вы
найдёте в замечательной книжке Я. С. Дубнова "Ошибки в геометрических доказательствах" (ссылка).
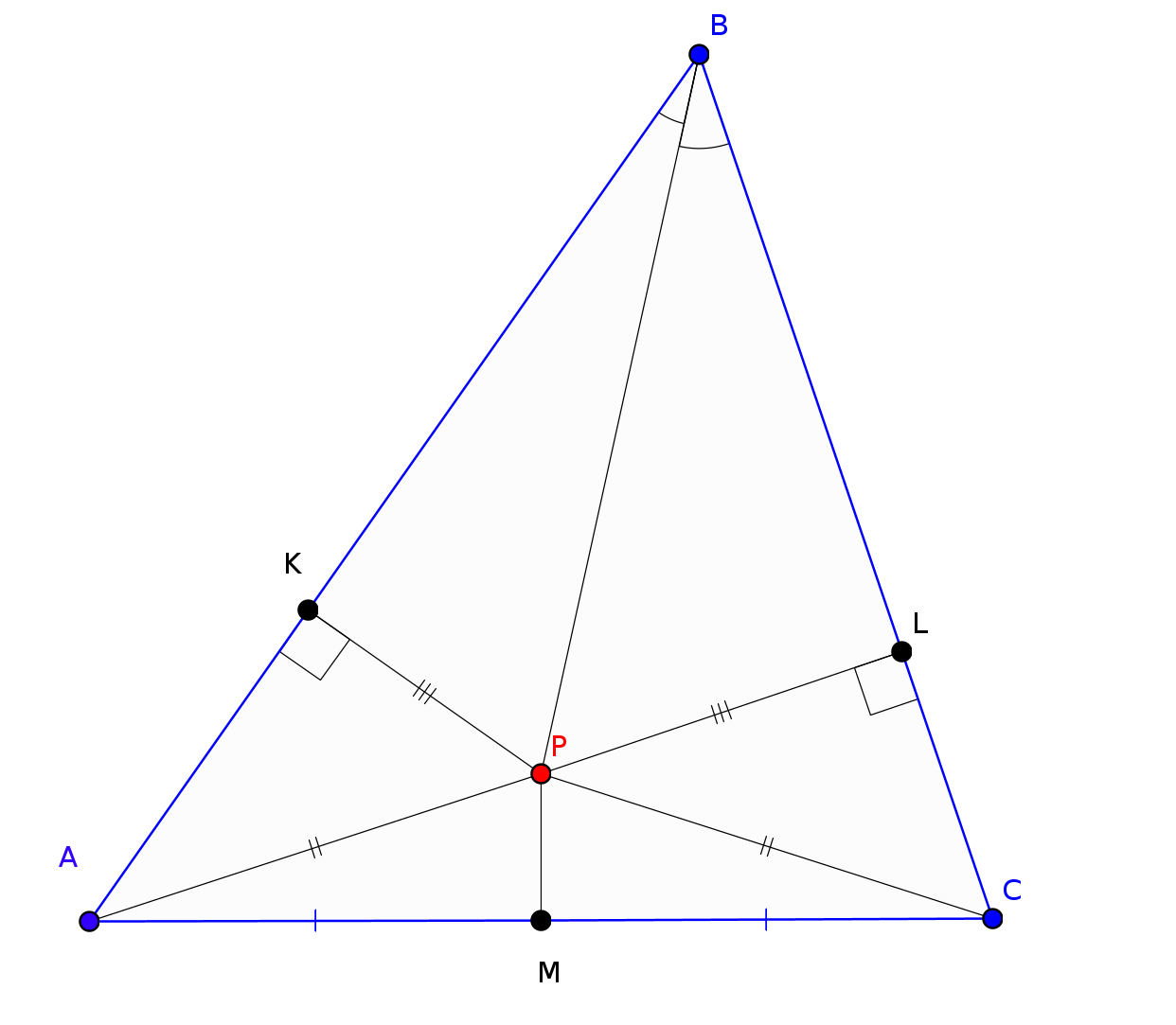
Пусть в треугольнике $ABC$ серединный перпендикуляр к стороне $AC$ и биссектриса угла $B$ пересекаются в точке $P$(см. рисунок).
Пусть $M$ – середина стороны $AC$; $K$ и $L$ – основания
перпендикуляров, опущенных из точки $P$ на стороны $AB$ и $AC$.
Заметим, что $\triangle KBP=\triangle LBP$, т.к. точка
$P$ лежит на биссектрисе $\angle ABC$, поэтому $BK=BL$ С другой стороны,
точка $P$ лежит на серединном перпендикуляре к стороне $AC$,
поэтому $AP=CP$. Получаем, что и
$\triangle APK=\triangle CPL$(по катету и гипотенузе).
Следовательно, $AK=CL$.
Таким образом, $AB=AK+BK=CL+BL=CB$.
Аналогично, можно показать, что и $AC=BC$, т.е. мы доказали "лемму" для любого треугольника!