• Куб и его развертка
• Пространственное воображение
• Разные задачи по геометрии
• Геометрия в пространстве
• Необычная геометрия
• Пространственное воображение
• Задачи про коз
• Углы
• Точки и прямые

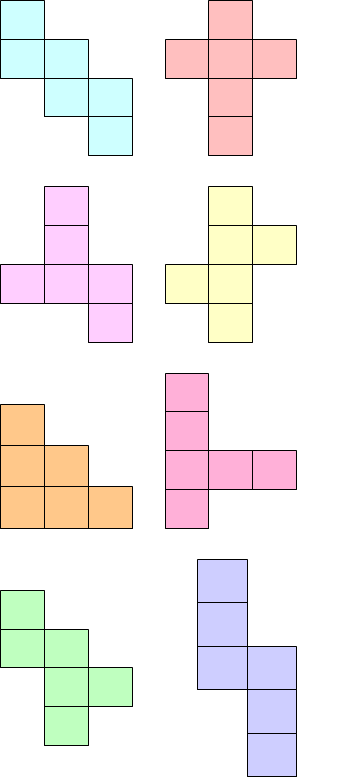
Куб и его развертка

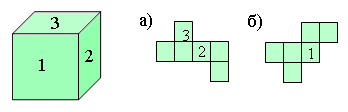
1. Выберите кубик соответствующий данной развертке.
   
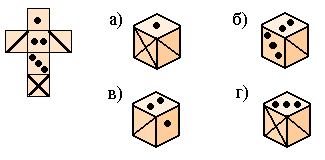
2. Из фигур на рисунке к задаче выберите те, которые являются развертками куба. Вырежьте их и покажите, как из них склеить куб.
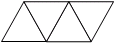
3. У Буратино была бумага, с одной стороны оклеенная полиэтиленом. Он сделал заготовку, изображенную на рисунке, чтобы склеить из нее пакет для молока. Лиса Алиса сказала, что может сделать другую заготовку и склеить такой же пакет. Какую?
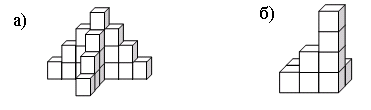
4. Изображенные на рисунке тела состоят из кубиков. Сколько кубиков в каждом из них?
   
5. На видимых гранях куба проставлены числа 1, 2 и 3. А на развертках — два из названных чисел или одно. Расставьте на развертках куба числа 1, 2, 3, 4, 5, 6 так, чтобы сумма чисел на противоположных гранях была равна 7.
   
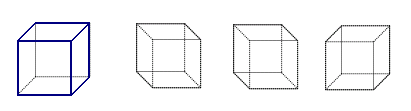
6. Пунктирными линиями на рисунке обозначены невидимые ребра куба. Соответственно, сплошными линиями показаны видимые линии. Мы смотрели на куб справа сверху. На рисунках а, б, в, проведите сплошные линии так, чтобы куб был виден
   1. справа снизу;
   2. слева сверху;
   3. слева снизу.
   
   

   Дополнительные задачи

7. Деревянный куб покрасили снаружи синей краской. После этого каждое ребро поделили на 5 частей и распилили данный куб на маленькие с ребром в 5 раз меньше. Сколько получилось маленьких кубиков?
   1. У скольких кубиков окрашены три грани?
   2. Две грани?
   3. Одна грань?
   4. Ни одной?
8. Отрезок, соединяющий две наиболее удаленные друг от друга вершины куба, называется его диагональю. Как измерить диагональ непустого куба, используя линейку и имея в наличии три таких куба?

Рисунок к задаче 2

---

Пространственное воображение

1. На большом круглом торте сделали 10 разрезов так, что каждый разрез идет от края до края и проходит через центр торта. Сколько получилось кусков?
2. У хозяйки был круглый торт с розочками из крема. Она разрезала его на части так, чтобы в каждой части была одна розочка. Всего она сделала три разреза. Сколько розочек могло быть на торте?
3. На какое наибольшее количество частей можно разрезать головку сыра тремя разрезами?
4. Можно ли испечь такой пирог, который может быть разделен одним прямолинейным разрезом на 4 части?
5. На прямоугольном торте лежит круглая шоколадка. Как разрезать торт на две равные части так, чтобы и шоколадка поделилась пополам?
6. На глобусе проведены 17 параллелей и 24 меридиана. На сколько частей разделена поверхность глобуса? (Меридиан — дуга, соединяющая Северный полюс с Южным. Параллель — это окружность, параллельная экватору.)
7. Можно ли расположить пять одинаковых монет так, чтобы каждая касалась трех других?

   Дополнительные задачи

8. Квадратную салфетку сложили пополам, а затем полученный прямоугольник еще раз сложили пополам. Получившийся квадратик разрезали ножницами по прямой. На сколько частей могла распасться салфетка?
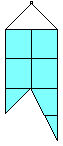
9. В стене имеется маленькая дырка (точка). У хозяина есть флажок следующей формы (см. рисунок). Покажите на рисунке все точки, в которые можно вбить гвоздь, так чтобы флажок закрывал дырку.
10. На плоском столе расположите 4 стакана, так чтобы попарные расстояния между центрами донышек стаканов были равны.

---

Разные задачи по геометрии

1. Вдоль двух прямолинейных парковых аллей посажены пять дубов — по три вдоль каждой аллеи (см. план парка). Садовник хочет проложить еще две аллеи так, чтобы по-прежнему вдоль каждой росли три дуба. Известно также, что у садовника есть только один саженец дуба. Где ему его посадить и где нужно проложить новые аллеи?
2. Можно ли квадратный лист бумаги размером 2x2 сложить так, чтобы его можно было разрезать на 4 квадрата 1x1 одним взмахом ножницами?
3. В углах квадратного бассейна стоят 4 столба. Можно ли расширить бассейн так, чтобы столбы остались на суше, площадь бассейна увеличилась бы в 2 раза, а форма осталась квадратной?
4. Кольца Борромео. Однажды итальянский вельможа Карло Борромео заказал сделать своему роду герб, на котором была бы изображена цепочка из трех переплетенных колец.
   Цепочка по замыслу вельможи должна быть такой: если ее собрать из трех бумажных колец, и разрезать любое одно звено, то она распалась бы на три части. Художники сказали, что такое невозможно, и предложили цепочку из трех колец, распадающуюся на три части при разрезании одного конкретного звена. Однако Борромео придумал, как собрать из трех колец нужную ему цепочку.
   а) Приведите пример цепочки, которую могли предложить художники Карло Борромео
   б) Изобразите герб рода Борромео.
5. Даны две палочки. Их можно прикладывать друг к другу и делать отметки. Как с помощью этих операций выяснить, что больше — длина более короткой палочки, или 2/3 длины более длинной палочки?
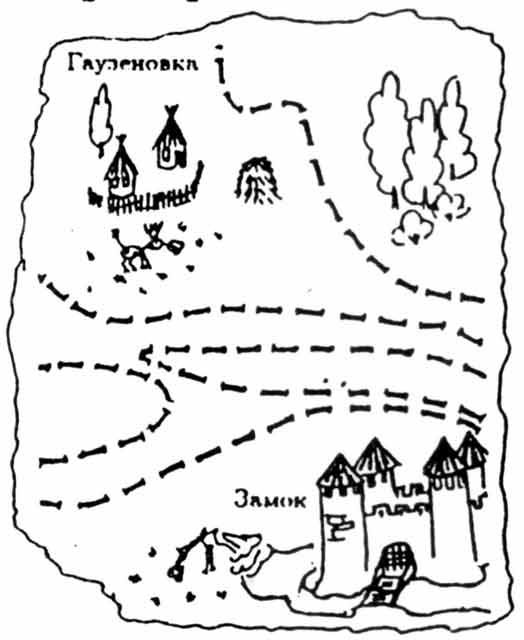
6. Давным-давно барон Мюнхгаузен обнес свои владения забором и нарисовал на карте. Забор изображен несамопересекающейся замкнутой ломаной, внутри которой — владения барона. Барон забыл, входит ли в его владения деревня Гаузеновка. Он смог найти лишь обрывок карты, на который попали его замок, деревня Гаузеновка и часть забора, проходящая по этому участку. Выясните, входит ли деревня во владения барона.
   
7. Из книги, состоящей из трех листов, вырежьте лист Мебиуса. Листом Мебиуса называется полоска с любыми краями, перекрученная один раз и склеенная.

   Дополнительные задачи

8. В цирк привезли девять тигров, которых поместили в загон, имеющий форму квадрата. Изобразите, каким образом внутри загона можно установить две решетки, каждая из которых также огораживает участок квадратной формы, чтобы изолировать хищников друг от друга (то есть, чтобы в результате загон разделился на девять частей)?
9. Как с помощью наименьшего количества прямолинейных разрезов разрезать квадрат 3x3 на единичные квадраты, если
   a) части нельзя накладывать (каждый раз можно разрезать только одну часть)
   б) части перед разрезанием можно накладывать друг на друга.
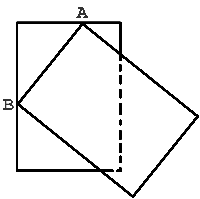
   в) перед разрезанием квадрат можно сложить?
10. Листок календаря частично закрыт предыдущим оторванным листком (см. рисунок). Вершины A и B верхнего листка лежат на сторонах нижнего листка. Четвёртая вершина нижнего листка не видна — она закрыта верхним листком. Верхний и нижний листки равны между собой. Какая часть нижнего листка больше — закрытая или открытая?

---

Геометрия в пространстве

1. Сложите куб из а) шести предложенных вам фигурок б) трех предложенных вам фигурок (фигурки даст преподаватель).
2. Придумайте и покажите, как можно разрезать куб на три пирамиды.
3. Из кубика Рубика 3x3x3 удалили центральный шарнир и восемь угловых кубиков. Можно ли оставшуюся фигуру из 18 кубиков составить из шести брусков размером 3x1x1?
4. Как из семи «уголков», каждый из которых склеен из трёх кубиков 1x1x1, и шести отдельных кубиков 1x1x1 cоставить большой куб 3x3x3? Можно ли это сделать так, чтобы все отдельные кубики оказались в серединах граней большого куба?
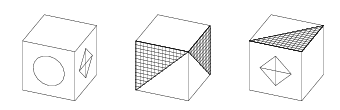
5. Придумайте такую раскраску граней кубика, чтобы в трёх различных положениях он выглядел так, как это показано на рисунке. (Укажите, как раскрасить невидимые грани, или нарисуйте развёртку.)
6. На столе лежит кубик, на его верхней стороне нарисована картинка. Кубик несколько раз перекатывали по столу через ребро, после чего он вновь оказался на прежнем месте. Могло ли оказаться, что картинка повернута на 180 градусов по сравнению с исходным положением?

   Дополнительные задачи

7. Некоторые ребра куба красные, а остальные — черные. При этом в каждую вершину приходит не более одного красного ребра. Какое наибольшее количество красных ребер может быть у такого куба?
8. В какое наименьшее количество красок можно покрасить ребра а) куба б) тетраэдра в) октаэдра так, чтобы каждое ребро было покрашено одной краской и любые два ребра, имеющие общую вершину, были бы покрашены в разные цвета?
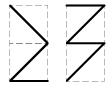
9. Если смотреть на аквариум спереди, то рыбка проплыла, как показано на левом рисунке. А если справа — то как на правом рисунке. Нарисуйте вид сверху.

На рисунке изображены развертки фигурок, необходимых для решения задачи 1.

---

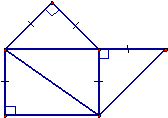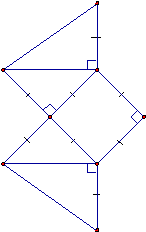Необычная геометрия

1. Разрежьте изображённую на рисунке фигуру на две одинаковые части.
   
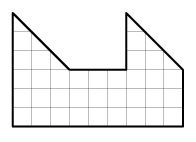
2. Поверхность кубика с ребром 1 можно оклеить шестью бумажными квадратами, каждый из которых имеет площадь 1. А можно ли оклеить кубик 12 бумажными квадратами, каждый из которых имеет площадь 1/2?
3. На листе бумаги размером 3´4 сделали разрезы так, чтобы он при этом не распался, но им стало возможно оклеить кубик размером 1´ 1´ 1 в два слоя. Как это сделали?
4. Все стенки и дно картонной коробки (без крышки) представляют собой квадраты, площадь каждого из которых равна 1. Разрежьте коробку на три куска так, чтобы из них можно было сложить квадрат.
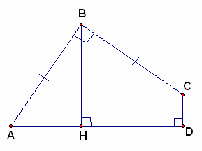
5. В четырехугольнике ABCDE (см. рисунок слева) углы ABC и ADC равны 90^o, стороны AB и BC равны и длина перпендикуляра BH равна 1. Найдите площадь этого четырехугольника.

6. Найдите сумму величин углов MAN, MBN, MCN, MDN и MEN, нарисованных на клетчатой бумаге так, как это показано на рисунке справа.
   
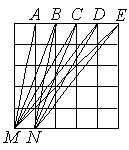
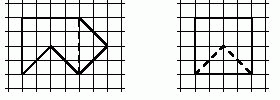
7. Серёжа придумал фигуру, которую легко разрезать на две части и сложить из них квадрат (см. рис.). Покажите, как по-другому разрезать эту фигуру на две части, из которых тоже можно сложить квадрат.
   

---

Пространственное воображение

1. У Пети есть три фигуры, вырезанные из бумаги. Каждая из них с одной стороны белая, а с другой — серая. Какие из пяти прямоугольников, изображенных на рисунке, нельзя сложить из этих фигур?
   
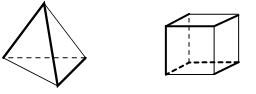
2. а) Тетраэдр б) куб разрезали по ребрам, выделенным жирными линиями (см. рисунки) и развернули. Нарисуйте получившиеся развертки.
   
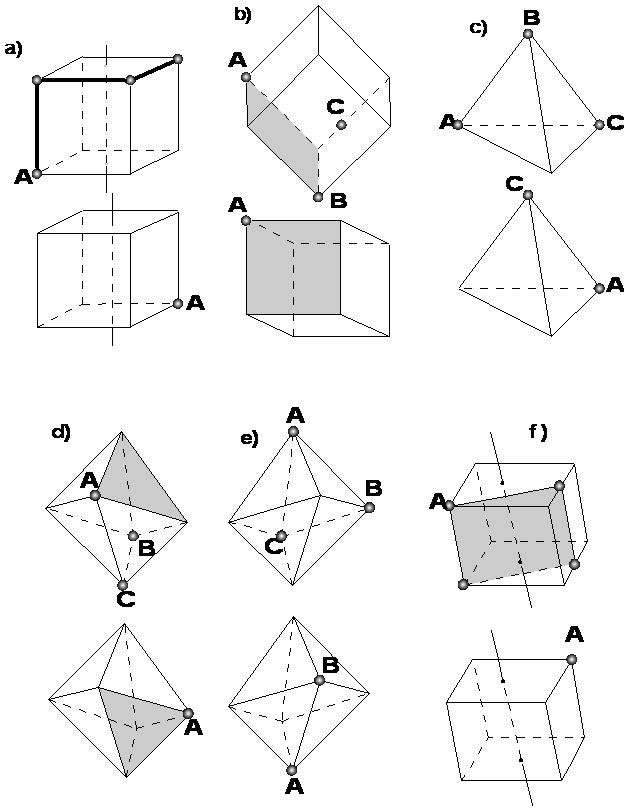
3. На каждом рисунке изображены два различных положения куба с заданной осью поворота (сверху — до поворота, снизу — после поворота). На верхнем кубе отмечены две его вершины, а на нижнем указано положение лишь одной из них. Отметьте положение второй вершины.
4. На каждом рисунке изображены два различных положения многогранника: куба, тетраэдра или октаэдра. На верхнем рисунке дано его исходное положение, на втором — после некоторого перемещения в пространстве. На первом рисунке отмечены некоторые элементы многогранника. Отметьте их на втором.
5. Представьте, что куб стоит на столе на одной своей вершине (так, что верхняя вершина расположена точно над нижней) и освещён прямо сверху. Какая в этом случае получается тень от куба? Нарисуйте ее.
6. Из квадрата 5x5 вырезали центральную клетку. Разрежьте получившуюся фигуру на две части, в которые можно завернуть куб 2x2x2.

   Дополнительные задачи

7. Составьте куб 3x3x3 из красных, жёлтых и зелёных кубиков 1x1x1 так, чтобы в любом бруске 3x1x1 были кубики всех трёх цветов.
8. Петя хочет изготовить необычную игральную кость, которая, как обычно, должна иметь форму куба, на гранях которого нарисованы точки (на разных гранях разное число точек), но при этом на любых двух соседних гранях число точек должно различаться по крайней мере на два (при этом разрешается, чтобы на некоторых гранях оказалось больше шести точек). Сколько всего точек необходимо для этого нарисовать? (Укажите минимальное количество, приведите пример их расположения на гранях и докажите, что меньшим числом обойтись нельзя.)
9. Из полоски бумаги шириной 1 см склеили цилиндрическое кольцо с длиной окружности 4 см. Можно ли из этого кольца изготовить квадрат, имеющий площадь: а) 1 см²; б) 2 см² ? Бумагу разрешается склеивать, складывать, но НЕЛЬЗЯ резать.

   Рисунок к задаче 3.

   

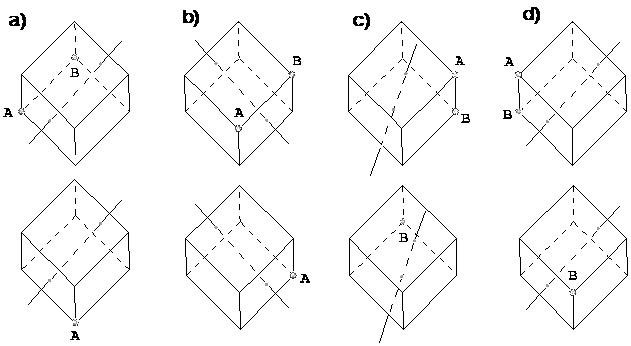
   Рисунок к задаче 4.

   

Задачи про коз

Первая часть этого занятия посвящена козам. Они прожорливы и съедают все, до чего могут дотянуться. Поэтому коз держат на привязи.

1. Нарисуйте участок луга, который выест коза, привязанная верёвкой к одиноко стоящему на лугу колышку.
2. Математик прогуливался по лугу, держа козу на поводке длины 1 м. Путь математика имел вид прямоугольника размером 3 м × 5 м. Нарисуйте участок, на котором могла побывать при этом коза, не обрывая поводка.
3. Одна коза съедает всю траву на участке за два часа, а вторая - за три часа. За какое время съедят всю траву на участке обе козы?
4. Удержите козу на участке изображенной формы, показнной на рисунке . (привяжите её с помощью верёвок и колышков так, чтобы она могла есть траву лишь внутри некоторого участка).
5. На лугу между двумя колышками натянем верёвку. У второй верёвки один конец привяжем к ошейнику козы, а на другом сделаем петлю, скользящую по первой верёвке. Какой участок выест коза?
6. Удержите козу а) в полукруге; б) в квадрате; в) в данном прямоугольнике.
7. Удержите козу в а) треугольнике; б) равностороннем шестиугольнике.
8. Введём в действие собак: будем привязывать их к колышкам, а они будут мешать козе есть. а) Как одной собакой удержать козу в кольце? б) А как - в полукруге? в) Удержите непривязанную козу с помощью собак в треугольнике.
9. Как действовать, чтобы "ограничить" козу заданным выпуклым многоугольником ?
10. Как заставить козу съесть сектор, используя не более а) семи; б) пяти колышков?
11. Какой участок съест коза, если ее привязать к проволочному контуру в форме креста?
12. Как одной собакой удержать непривязанную козу в полукруге?
13. Как с помощью двух собак удержать козу в кресте или в полумесяце?
14. Подумайте, как действовать, чтобы "ограничить" непривязанную козу с помощью собак заданным многоугольником (не обязательно выпуклым)?

Углы

1. На сколько градусов поворачивается за одну минуту минутная стрелка? Часовая стрелка? Найдите угол между часовой и минутной стрелками в 3 часа 20 минут.
2. Через точку на плоскости провели 7 прямых, после чего плоскость разрезали по этим прямым на углы. Верно ли, что хотя бы один из этих углов меньше 26 градусов ?
3. Имеется угольник с углом в 19 градусов , а другие углы неизвестны. Как построить с его помощью угол в 1 градус?
4. Можно ли провести из одной точки на плоскости пять лучей так, чтобы среди образованных ими углов было ровно четыре острых? Рассматриваются углы не только между соседними, но и между любыми двумя лучами.
5. В Совершенном городе шесть площадей. Каждая площадь соединена прямыми улицами ровно с тремя другими площадями. Никакие две улицы в городе не пересекаются. Из трёх улиц, отходящих от каждой площади, одна проходит внутри угла, образованного двумя другими. Начертите возможный план такого города.
6. Есть три треугольника: остроугольный, прямоугольный и тупоугольный. Саша взял себе один треугольник, а Боря~--- два оставшихся. Оказалось, что Боря может приложить (без наложения) один из своих треугольников к другому, и получить треугольник, равный Сашиному. Какой из этих треугольников взял Саша?
7. Придумайте комнату такой формы, чтобы в ней можно было указать точку, из которой ни одна из стен не видна полностью.
8. В вершинах четырехугольника расположены четыре прожектора, каждый освещает угол в 90 градусов. Докажите, что можно так направить каждый из прожекторов, что вся плоскость окажется освещенной.
9. У Васи есть пластмассовый угольник (без делений) с углами 30 градусов, 60 градусов и 90 градусов. Ему нужно построить угол в 15 градусов. Как это сделать, не используя других инструментов?
10. Кролик, готовясь к приходу гостей, повесил в трёх углах своей многоугольной норы по лампочке. Пришедшие к нему Винни-Пух и Пятачок увидели, что не все горшочки с мёдом освещены. Когда они полезли за мёдом, две лампочки разбились. Кролик перевесил оставшуюся лампочку в некоторый угол так, что вся нора оказалась освещена. Могло ли такое быть? (Если да, нарисуйте пример, если нет, обоснуйте ответ.)

Точки и прямые

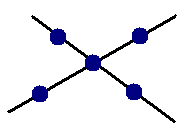
1. Нарисуйте на плоскости шесть прямых так, чтобы они пересекались ровно в шести различных точках.
2. Начертите 7 прямых и отметьте на них 8 точек так, чтобы на каждой прямой лежало ровно 3 отмеченных точки. (Можно отмечать как точки пересечения прямых, так и точки, которые лежат только на одной прямой.)
3. На плоскости провели 6 прямых и отметили несколько точек так, что на каждой прямой оказалось ровно по три отмеченных точки. Какое наименьшее число точек могло быть отмечено?
4. Отметьте на плоскости 6 точек и провести 6 прямых так, чтобы на любой прямой было две точки и по обе стороны от нее лежало по две точки.
5. Пусть на плоскости отмечено несколько точек. Назовём прямую нечестной, если она проходит ровно через три отмеченные точки и по разные стороны от неё отмеченных точек не поровну. (В частности, с одной стороны от прямой может вообще не лежать точек.) Отметьте на плоскости 7 точек и проведите для них 5 нечестных прямых
6. На плоскости провели 10 прямых и отметили их точки пересечения. Какое наибольшее количество точек могло получиться?
7. Коля провёл на листе бумаги 4 прямых линии, которые пересеклись в 6 попарно различных точках. Петя отметил маркером эти точки, а сами линии стёр. Вася может провести прямую линию через любые две из отмеченных точек, но не может заранее оценить, через какие из остальных отмеченных точек она пройдёт. Вася хочет восстановить Колины линии, проведя как можно меньше прямых. Какое количество прямых ему придётся провести в наихудшем случае?

---

МЦНМО