Наглядная геометрия > Филиал Малого Мехмата в школе 218

Необычная геометрия

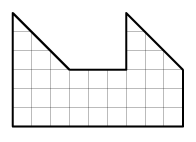
1. Разрежьте изображённую на рисунке фигуру на две одинаковые части.
   
2. Поверхность кубика с ребром 1 можно оклеить шестью бумажными квадратами, каждый из которых имеет площадь 1. А можно ли оклеить кубик 12 бумажными квадратами, каждый из которых имеет площадь 1/2?
3. На листе бумаги размером 3´4 сделали разрезы так, чтобы он при этом не распался, но им стало возможно оклеить кубик размером 1´ 1´ 1 в два слоя. Как это сделали?
4. Все стенки и дно картонной коробки (без крышки) представляют собой квадраты, площадь каждого из которых равна 1. Разрежьте коробку на три куска так, чтобы из них можно было сложить квадрат.
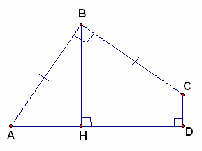
5. В четырехугольнике ABCDE (см. рисунок слева) углы ABC и ADC равны 90^o, стороны AB и BC равны и длина перпендикуляра BH равна 1. Найдите площадь этого четырехугольника.

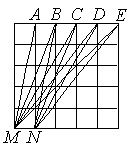
6. Найдите сумму величин углов MAN, MBN, MCN, MDN и MEN, нарисованных на клетчатой бумаге так, как это показано на рисунке справа.
   
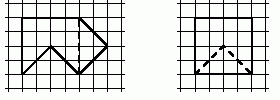
7. Серёжа придумал фигуру, которую легко разрезать на две части и сложить из них квадрат (см. рис.). Покажите, как по-другому разрезать эту фигуру на две части, из которых тоже можно сложить квадрат.