Наглядная геометрия > Филиал Малого Мехмата в школе 218

Разные задачи по геометрии

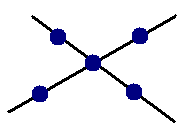
1. Вдоль двух прямолинейных парковых аллей посажены пять дубов — по три вдоль каждой аллеи (см. план парка). Садовник хочет проложить еще две аллеи так, чтобы по-прежнему вдоль каждой росли три дуба. Известно также, что у садовника есть только один саженец дуба. Где ему его посадить и где нужно проложить новые аллеи?
2. Можно ли квадратный лист бумаги размером 2x2 сложить так, чтобы его можно было разрезать на 4 квадрата 1x1 одним взмахом ножницами?
3. В углах квадратного бассейна стоят 4 столба. Можно ли расширить бассейн так, чтобы столбы остались на суше, площадь бассейна увеличилась бы в 2 раза, а форма осталась квадратной?
4. Кольца Борромео. Однажды итальянский вельможа Карло Борромео заказал сделать своему роду герб, на котором была бы изображена цепочка из трех переплетенных колец.
   Цепочка по замыслу вельможи должна быть такой: если ее собрать из трех бумажных колец, и разрезать любое одно звено, то она распалась бы на три части. Художники сказали, что такое невозможно, и предложили цепочку из трех колец, распадающуюся на три части при разрезании одного конкретного звена. Однако Борромео придумал, как собрать из трех колец нужную ему цепочку.
   а) Приведите пример цепочки, которую могли предложить художники Карло Борромео
   б) Изобразите герб рода Борромео.
5. Даны две палочки. Их можно прикладывать друг к другу и делать отметки. Как с помощью этих операций выяснить, что больше — длина более короткой палочки, или 2/3 длины более длинной палочки?
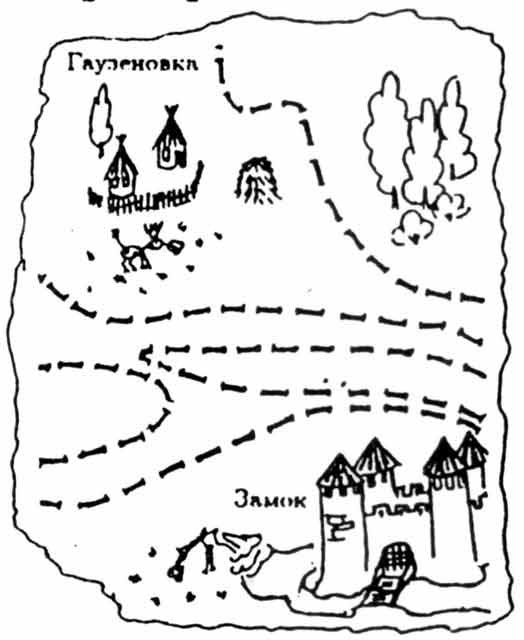
6. Давным-давно барон Мюнхгаузен обнес свои владения забором и нарисовал на карте. Забор изображен несамопересекающейся замкнутой ломаной, внутри которой — владения барона. Барон забыл, входит ли в его владения деревня Гаузеновка. Он смог найти лишь обрывок карты, на который попали его замок, деревня Гаузеновка и часть забора, проходящая по этому участку. Выясните, входит ли деревня во владения барона.
   
7. Из книги, состоящей из трех листов, вырежьте лист Мебиуса. Листом Мебиуса называется полоска с любыми краями, перекрученная один раз и склеенная.

   Дополнительные задачи

8. В цирк привезли девять тигров, которых поместили в загон, имеющий форму квадрата. Изобразите, каким образом внутри загона можно установить две решетки, каждая из которых также огораживает участок квадратной формы, чтобы изолировать хищников друг от друга (то есть, чтобы в результате загон разделился на девять частей)?
9. Как с помощью наименьшего количества прямолинейных разрезов разрезать квадрат 3x3 на единичные квадраты, если
   a) части нельзя накладывать (каждый раз можно разрезать только одну часть)
   б) части перед разрезанием можно накладывать друг на друга.
   в) перед разрезанием квадрат можно сложить?
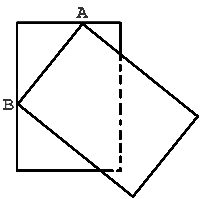
10. Листок календаря частично закрыт предыдущим оторванным листком (см. рисунок). Вершины A и B верхнего листка лежат на сторонах нижнего листка. Четвёртая вершина нижнего листка не видна — она закрыта верхним листком. Верхний и нижний листки равны между собой. Какая часть нижнего листка больше — закрытая или открытая?