Гомотетия
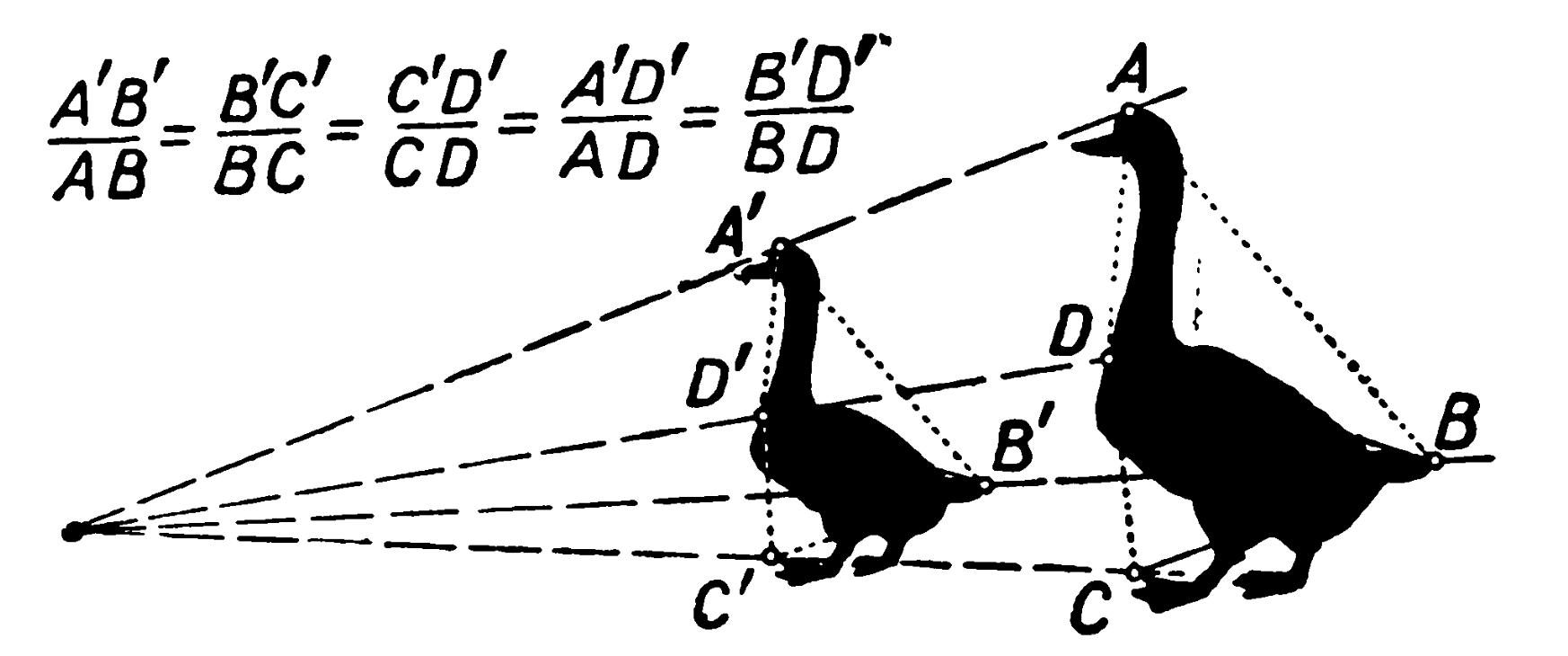
Листки списком
- Построения. В первом листке предлагается несколько задач на построение, при решении этих задач гомотетия возникает естественно. Никаких определений тут мы не даём.
- Первые доказательства. Начинаем решать задачи на доказательство с использованием гомотетии. Во всех задача достаточно однократного выполнения гомотетии. Задачи 3 и 6 — классические результаты Л. Эйлера.
- Окружности. Как взаимодействует гомотетия и окружность? Как построить центр гомотетии двух окружностей? Как это использовать?
 Для чтения горячо рекомендуем всем статью Г. Б. Филипповского Олимпиадная лемма Архимеда
Для чтения горячо рекомендуем всем статью Г. Б. Филипповского Олимпиадная лемма Архимеда
- Лемма о вписанной окружности. Весь сюжет разворачивается вокруг следующей конструкции:
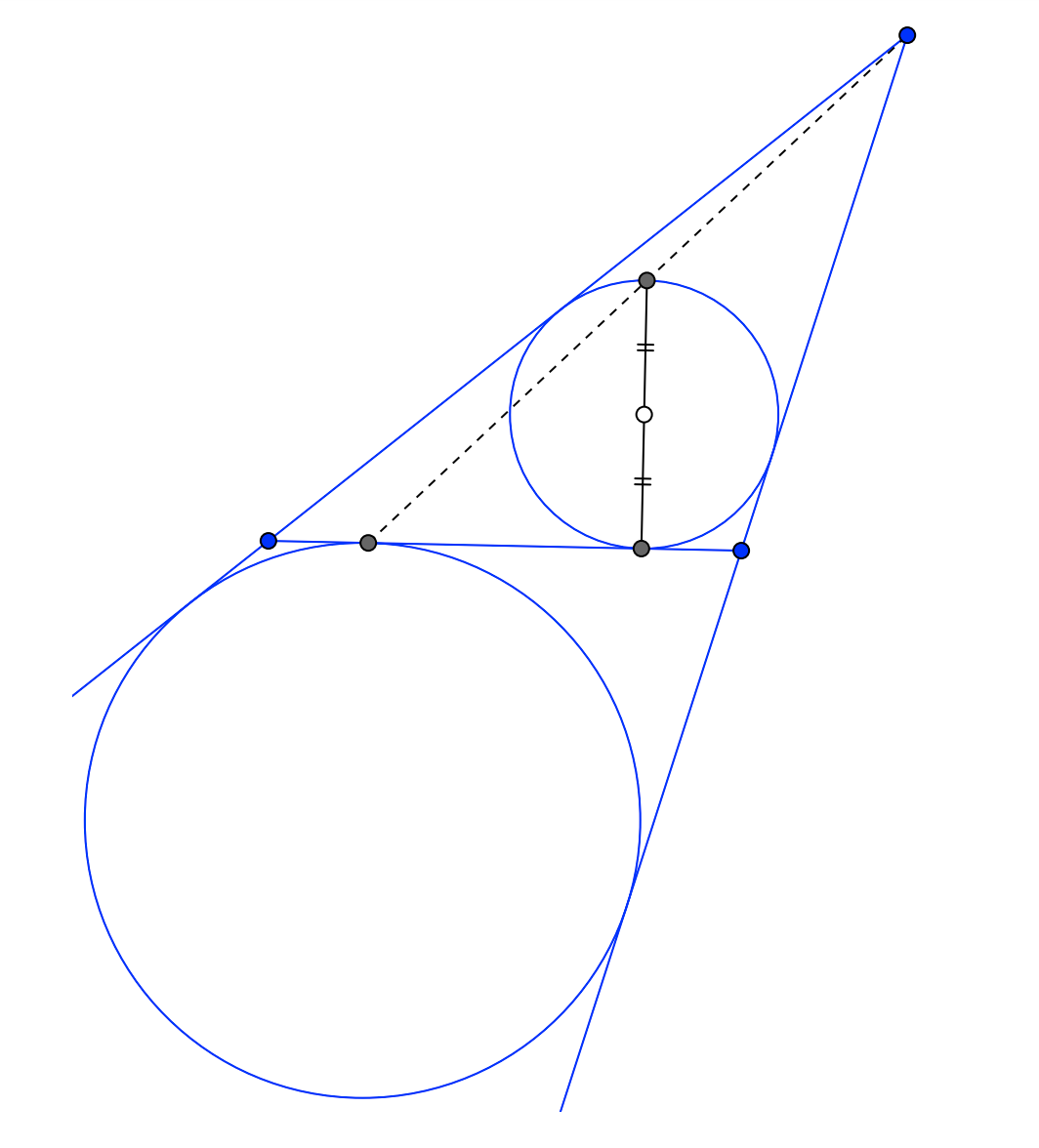
 Тут для чтения советуем статьи А.Д. Блинкова, Ю.А. Блинкова "Вневписанная окружность",
Тут для чтения советуем статьи А.Д. Блинкова, Ю.А. Блинкова "Вневписанная окружность",
Г.Б. Филипповского, А. Карлюченко "Об одной замечательной прямой" - "Параллельные" треугольники. Если в треугольниках стороны попарно параллельны, то прямые, соединяюищие соответственные вершины, пересекаются в одной точке(либо параллельны).
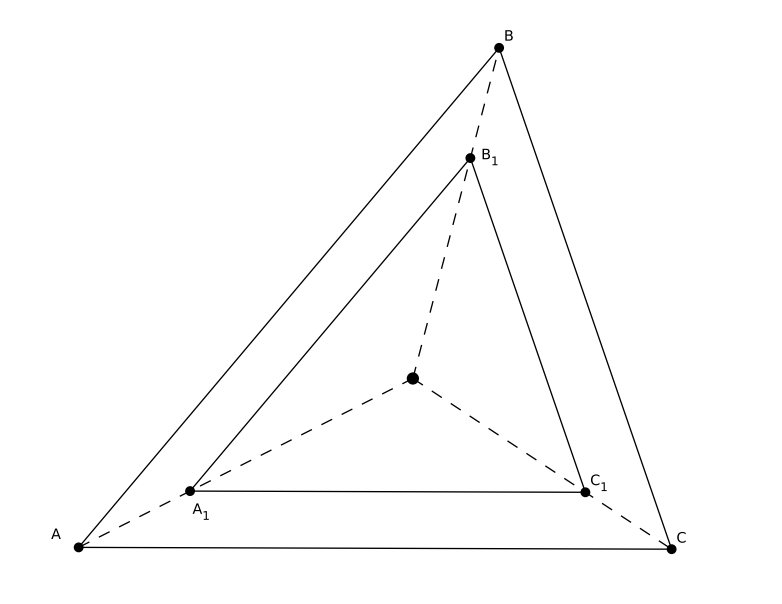
 Для изучения рекомендуем насыщенную статью Ю.А. Блинков
Для изучения рекомендуем насыщенную статью Ю.А. Блинков
"Ортоцентр, середина стороны, точка пересечения касательных и ещё одна точка!"
Для связи: shvetsov @ 179. ru