Семинар по геометрии имени И.Ф. Шарыгина. 25 февраля 2010 года

Докладчик: Аркадий Борисович Скопенков (МГУ).

Тема доклада: «Объемная однородность»

Аннотация:

Подмножество N плоскости называется аффинно объемлемо однородным, если для любых двух точек x, y принадлежащих N существует аффинное преобразование плоскости переводящее x в y и N в себя. Приводится следующий результат (Д. Реповша, Е. Щепина и автора). Аффинно объемлемо однородное замкнутое подмножество плоскости является либо набором изолированных точек, либо объединением изолированных дифференцируемых кривых. Приводится обсуждения, следствия и обобщения этого результата. Например: если график непрерывной функции 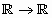аффинно объемлемо однороден, то эта функция дифференцируема. В конце приводятся и неэлементарные следствия (в частности, получается простое доказательство гладкой версии гипотезы Гильберта-Смита о топологических группах, возникшей при решении 5-й проблемы Гильберта).

Для понимания большей части доклада достаточно владеть понятием непрерывности (в частности, понятиями открытых и замкнутых множеств прямой и плоскости).

Приглашаем постоянных участников семинара и всех желающих!