Семинар по геометрии имени И.Ф. Шарыгина. 29 октября 2009 года
Докладчик: Игорь Николаевич Шнурников (МГУ, мех-мат).
Тема доклада: «На сколько частей можно разделить плоскость прямыми?»
Аннотация:
На какое число областей n
прямых могут разделить плоскость?
Если все прямые параллельны, то на n+1
область, если прямые — общего положения, то на
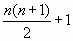 область.
Это — наименьшее и наибольшее возможное
число областей.
Оказывается, однако, что далеко не все
промежуточные значения реализуются. Какие же
числа из отрезка
область.
Это — наименьшее и наибольшее возможное
число областей.
Оказывается, однако, что далеко не все
промежуточные значения реализуются. Какие же
числа из отрезка
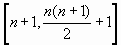 могут служить числом областей
разбиения? Б. Грюнбаум в 1972 году полагал, что
все числа из отрезка [3n—1,4n—9] не реализуются
при
могут служить числом областей
разбиения? Б. Грюнбаум в 1972 году полагал, что
все числа из отрезка [3n—1,4n—9] не реализуются
при 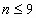 . Н. Мартинов в 1993 году предложил
формулу для всех возможных чисел областей
разбиения. В.И. Арнольд в 2007 году (не зная о
работах своих предшественников) вывел
формулу Н. Мартинова и частично ее доказал.
Мы представляем полное решение этой задачи.
Доклад доступен для понимания
старшеклассникам.
. Н. Мартинов в 1993 году предложил
формулу для всех возможных чисел областей
разбиения. В.И. Арнольд в 2007 году (не зная о
работах своих предшественников) вывел
формулу Н. Мартинова и частично ее доказал.
Мы представляем полное решение этой задачи.
Доклад доступен для понимания
старшеклассникам.
Приглашаем постоянных участников семинара и всех желающих!