Шестая Всероссийская олимпиада по геометрии имени Игоря Федоровича Шарыгина (2010 год)
Внимание! В задаче 15 исправлена опечатка.
Внимание! В задаче 8 исправлена опечатка
Приводим условия задач заочного тура шестой геометрической олимпиады им. И.Ф.Шарыгина.
В олимпиаде могут участвовать школьники 8–11 классов. В списке задач, приведенном ниже, после порядкового номера каждой задачи указано, учащимся каких классов (на момент проведения олимпиады) она предназначена. Впрочем, можно решать также задачи и для более старших классов (решенные задачи для младших классов при подведении итогов не учитываются).
Решения задач на русском языке должны быть посланы не позднее 1 апреля 2010 года.
Рекомендуется присылать решения по электронной почте в форматах pdf, doc или jpg на адрес geomolymp@mccme.ru. При этом во избежание потери работы нужно соблюдать следующие правила.
- Каждую работу следует посылать отдельным письмом.
- Если работа содержится в нескольких файлах, желательно присылать их в виде архива.
- В теме письма нужно написать "работа на олимпиаду им.Шарыгина", а в тексте
привести следующие сведения об участнике:
– фамилию, имя, отчество;
– полный почтовый адрес с индексом, телефон, E-mail;
– класс, в котором сейчас учится школьник;
– номер и адрес школы;
– ФИО учителей математики и/или руководителей кружка.
Если у Вас нет возможности прислать работу в электронном виде, пришлите ее простой
бандеролью (или принесите сами) в обычной тетради, не сворачивая тетрадь в трубку, по
адресу:
119002, Москва Г-002, Большой Власьевский пер., д. 11., МЦНМО. На олимпиаду
им. И.Ф.Шарыгина.
На обложке тетради обязательно укажите все сведения, перечисленные выше в п.3.
Решение каждой задачи начинайте с новой страницы: сначала надо переписать условие, затем записать решение, причем старайтесь писать подробно, приводя основные рассуждения и выкладки, делая аккуратные чертежи. Если задача на вычисления, в конце ее решения должен быть отчетливо выделенный ответ. Пишите аккуратно, ведь Вы же заинтересованы в том, чтобы Вашу работу можно было понять и справедливо оценить!
Если Вы пользуетесь в решении какой-то известной теоремой или фактом, приведенным в задаче из школьного учебника, можно просто на это сослаться (чтобы было понятно, какую именно теорему или факт Вы имеете в виду). Если же Вам необходим факт, не встречающийся в школьном курсе, его обязательно надо доказать (или сообщить, из какого источника он взят).
Ваши работы будут тщательно проверены, и Вы получите (не позднее середины мая 2010 г.) ответ жюри. Победители заочного тура — учащиеся 8–10 классов будут приглашены на финальный тур, который состоится летом 2010 года в г. Дубна под Москвой. Победители заочного тура — выпускники школ получат Грамоты оргкомитета олимпиады.
Условия задач заочного тура
English version also available PDF, 90K
- (8) Существует ли треугольник, в котором одна сторона равна
какой-то из его высот, другая – какой-то из биссектрис, а третья
– какой-то из медиан?
- (8) В прямоугольном треугольнике ABC (угол C равен 90o)
биссектрисы AA1 и BB1 пересекаются в точке I. Пусть
O – центр описанной окружности треугольника CA1B1.
Докажите, что OI перпендикулярен AB.
- (8) Точки A', B', C' лежат на сторонах BC, CA, AB
треугольника ABC. Точка X такова, что
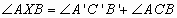 и
и 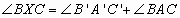 .
Докажите, что четырёхугольник XA'BC' – вписанный.
.
Докажите, что четырёхугольник XA'BC' – вписанный.
- (8) Диагонали вписанного четырёхугольника ABCD пересекаются в
точке N. Окружности, описанные вокруг треугольников ANB и
CND, повторно пересекают стороны BC и AD в точках A1,
B1, C1, D1. Докажите, что четырёхугольник
A1B1C1D1 вписан в окружность с центром N.
- (8–9) На высоте BD треугольника ABC взята точка E такая,
что угол AEC равен 90o. Точки O1 и O2 – центры
описанных окружностей треугольников AEB и CEB; F, L –
середины отрезков AC и O1O2. Докажите, что точки L, E,
F лежат на одной прямой.
- (8–9) На стороне BC равностороннего треугольника ABC взяты
точки M и N (M лежит между B и N) такие, что угол MAN равен 30o.
Описанные окружности треугольников AMC и ANB
пересекаются в точке K. Докажите, что прямая AK содержит центр
описанной окружности треугольника AMN.
- (8–9) Через вершину B треугольника ABC проведена прямая,
перпендикулярная медиане BM. Эта прямая пересекает высоты,
выходящие из A и C (или их продолжения), в точках K и N.
Точки O1 и O2 – центры описанных окружностей
треугольников ABK и CBN соответственно. Докажите, что
O1M=O2M.
- (8–10) В треугольнике ABC проведена высота AH. Точки Ib и Ic – центры вписанных окружностей треугольников ABH и ACH; L – точка касания вписанной окружности треугольника ABC со стороной BC. Найдите угол LIbIc.
- (8–10) Назовём точку внутри треугольника хорошей, если три чевианы через неё равны. В треугольнике ABC стороны AB и BC равны, а количество хороших точек нечётно. Чему оно может быть равно?
- (8–11) Дан треугольник ABC. С помощью двусторонней линейки, проведя не более восьми линий, постройте на стороне AB такую точку D, что AD/BD=BC/AC.
- (8–11) Выпуклый n-угольник разрезан на 3 выпуклых многоугольника. У одного из них n сторон, у другого – больше, чем n, у третьего – меньше, чем n. Каковы возможные значения n?
- (9) В прямоугольном треугольнике ABC AC – больший катет, CH – высота, проведенная к гипотенузе. Окружность с центром H и радиусом CH пересекает катет AC в точке M. Точка B' симметрична точке B относительно H. В точке B' восставлен перпендикуляр к гипотенузе, который пересекает окружность в точке K. Докажите, что: а) B'M || BC; б) AK – касательная к окружности.
- (9) В выпуклом четырехугольнике ABCD AB=BC. На диагонали BD выбрана точка K такая, что
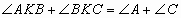 . Докажите, что
. Докажите, что 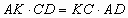 .
.
- (9–10) На стороне AD выпуклого четырехугольника ABCD нашлась такая точка M, что CM и BM параллельны AB и CD соответственно. Докажите, что
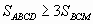 .
.
- (9–11) В остроугольном треугольнике ABC AA1, BB1 и CC1 – высоты. Прямые AA1 и B1C1 пересекаются в точке K. Окружности, описанные вокруг треугольников A1KC1 и A1KB1 вторично пересекают прямые AB и AC в точках N и L соответственно. Докажите, что а) сумма диаметров этих окружностей равна стороне BC. б) A1N/BB1+A1L/CC1=1.
- (9–11) В угол с вершиной A вписана окружность, касающаяся сторон угла в точках B и C. Прямая, проходящая через A, пересекает окружность в точках D и E. Хорда BX параллельна прямой DE. Докажите, что отрезок XC проходит через середину отрезка DE.
- (9–11) Постройте треугольник по высоте и биссектрисе, проведенным из одной вершины, и медиане, проведенной из другой вершины.
- (9–11) На хорде AC окружности w выбрали точку B. На отрезках AB и BC как на диаметрах построили окружности w1 и w2 с центрами O1 и O2, которые пересекают w второй раз в точках D и E соответственно. Лучи O1D и O2E пересекаются в точке F. Лучи AD и CE пересекаются в точке G. Докажите, что прямая FG проходит через середину AC.
- (9–11) Четырехугольник ABCD вписан в окружность с центром O. Точки P и Q диаметрально противоположны C и D соответственно. Касательные к окружности в этих точках пересекают прямую AB в точках E и F (A лежит между E и B, B – между A и F). Прямая EO пересекает AC и BC в точках X и Y, а прямая FO пересекает AD и BD в точках U и V. Докажите, что XV=YU.
- (10) Вписанная окружность остроугольного треугольника ABC касается его сторон AB, BC, CA в точках C1, A1, B1 соответственно. Пусть A2, B2 – середины отрезков B1C1, A1C1 соответственно, O – центр описанной окружности треугольника, P – одна из точек пересечения прямой CO с вписанной окружностью. Прямые PA2 и PB2 вторично пересекают вписанную окружность в точках A' и B'. Докажите, что прямые AA' и BB' пересекаются на высоте треугольника, опущенной на AB.
- (10–11) Дан выпуклый четырехугольник ABCD. Известно, что
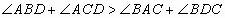 . Докажите, что
. Докажите, что
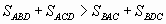 .
.
- (10–11) Окружность с центром F и парабола с фокусом F пересекаются в двух точках. Докажите, что на окружности найдутся такие четыре точки A, B, C, D, что прямые AB, BC, CD и DA касаются параболы.
- (10–11) Шестиугольник ABCDEF вписан в окружность. Известно, что
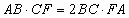 ,
, 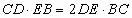 ,
, 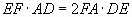 .
Докажите, что прямые AD, BE и CF
пересекаются в одной точке.
.
Докажите, что прямые AD, BE и CF
пересекаются в одной точке.
- (10–11) Дана прямая l в пространстве и точка A, не лежащая на ней. Для каждой прямой l', проходящей через A, построим общий перпендикуляр XY (Y лежит на l') к прямым l и l'. Найдите ГМТ точек Y.
- (11) Среди вершин двух неравных икосаэдров можно выбрать шесть, являющихся вершинами правильного октаэдра. Найдите отношение ребер икосаэдров.
- (8–10) В треугольнике ABC проведена высота AH. Точки Ib и Ic – центры вписанных окружностей треугольников ABH и ACH; L – точка касания вписанной окружности треугольника ABC со стороной BC. Найдите угол LIbIc.